1. Intro
위 링크를 참고하였고 코드작성에 큰 도움을 받을 수 있었다.
위 링크에서처럼 클래스를 활용하여 코드를 작성하면 코드 가독성이 좋을 것 같다. 하지만 나는 아직 객체지향 문법에 익숙치 않아 그냥 몇 함수들을 만들어 구현하였고 이것이 지금은 더 간단하고 효율적으로 보인다.
2. 구현결과
작성한 코드는 위 링크에 업로드하였다.
play횟수는 1만번을 진행하였다. 500번, 1천번에 대해서도 진행하였지만 SARSA의 Optimal Policy가 정확히 원하는 결과로 나오지 않아 그냥 1만번으로 확 늘려 진행하였고 교재와 같은 결과를 얻을 수 있었다.



하지만 교재에서 아래처럼 Sum of rewards during episode를 볼 수 있는데 이는 나와 다르게 나왔다.
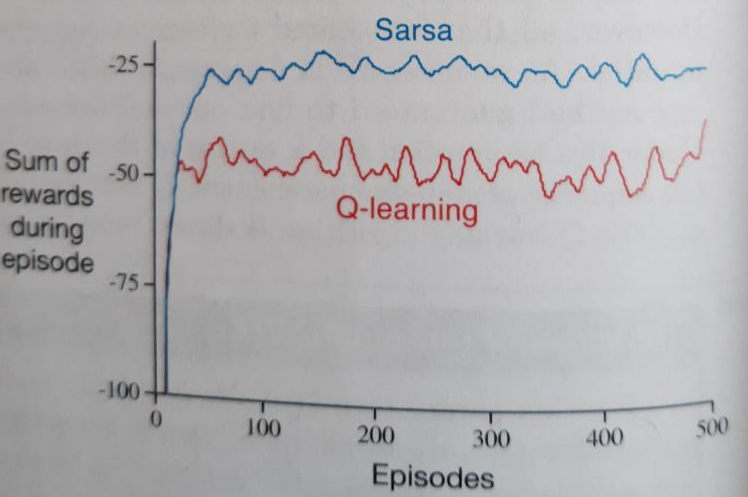

아무리 많은 play로 Q-value를 업데이트했다고 해도 실제 action을 취하는 policy는 SARSA와 Q-learning 모두 epsilon-greedy policy임에 따라 10%확률로 무조건 랜덤한 action을 취하게 된다. Cliff바로 옆의 최적경로를 대세로 움직이는 Q-learning에서는 보다 높은 확률로 Cliff로 빠지게 되고 -100보다 작은 reward를 얻어야 하는 것이 정상이다. 하지만 교재에서는 30번의 play이후 부터는 -60보다 큰 reward를 지속적으로 보여준다. 이 부분은 이해가 되지 않았다.
추가피드백)
교재에서 에피소드가 진행됨에 따라 -100의 reward를 얻지 않는 것처럼 보이는 이유는 그래프를 만들 때 평균처리를 했기 때문이다. 즉 n번째 에피소드에서의 rewardSum/n 값을 그래프에 나타낸 것으로 -100에 도달하지 않는 것이다.
하지만 교재와 같은 부분은 SARSA의 경우보다 Q-learning의 경우가 더 reward가 낮다는 것을 확인할 수 있다. 1만번의 play 끝자락인 9900~10000의 경우에 대해서 보면 더욱 뚜렷히 볼 수 있다. 이는 이론적으로도 Cliff를 따라 대세적으로 움직이는 Q-learning이 Cliff에 더 자주 빠져 -100에 가까운 reward를 더욱 자주 얻게 된다. 이와 반대로 SARSA의 경우 Cliff와 가장 떨어진 경로를 대세로 움직이므로 cliff에 빠질 활률이 매우 낮다. 아래에서는 한 번도 빠지지 않음을 볼 수 있다.

3. SARSA와 Q-learning의 Optimal 경로차이

'기계공학부 시절의 기록 > 강화학습일기' 카테고리의 다른 글
| 로봇 동작학습 참고할 연구들 (0) | 2021.12.04 |
|---|---|
| [MC BlackJack] 오류 수정 및 결과도출 (0) | 2021.11.13 |
| RL 개념 흐름 정리 (0) | 2021.11.11 |
| [MC BlackJack 결과 시각화] 학습결과 그래프로 나타내기 (0) | 2021.11.10 |
| [MC Blackjack-최종] 코드작성과 결과코드 및 실행영상 (2) | 2021.11.04 |



댓글