RL homework - MDP #1 Gambler's problem 이해하기 쉬운 코드

결과물은 아래의 깃허브주소에 업로드하였다.

GitHub - needs-searcher/RL_Example: This is my RL Example codes

 

인터넷 상에서 몇 코드들을 보았는데 코딩 초보자로서 이해하기가 힘들었다.

본 글에서는 직접 작성한, 보다 이해하기 쉬운 코드로 RL 교과서의 예제 Gambler's Problem을 해결하였다.

해당 코드는 아래부분 [2차코드]를 보면된다.

참고로, 주피터 노트북이나 파이썬 설치가 되어있지 않더라도 google colab을 이용해 언제든 코드를 작성하고 돌려볼 수 있다.

---

Gambler's Problem 게임룰

 

# 승 : 동전 앞면, 패 : 동전 뒷면

# State(현재 가진 돈)가 0 or 100이 되는 순간 Episode는 종료

# Action(게임에 거는 돈) = [1, 2, 3, ..., min(state, 100 - state)]

자신이 가진 돈보다 많이 걸 수 없고, state가 100이 되는 것이 목표이므로 98일 때 2보다 많은 돈을 걸 이유가 없다.

# gamma = 1

끝이 있는 유한한 Episodic한 문제이므로 gamma가 1로 주어졌다.

# R

다음 state가 100이 되는 경우에만 R = 1, 나머지는 모두 0

# state-value : 현재 state에서 이길 확률

# p = 0.4 : 동전 앞면이 나올 확률.

앞면이 나올 때 게임에 승리하여 건 돈만큼 얻을 수 있다.

 

value Iteration 식으로 문제를 해결한다.

---

필요개념 : Bellman Equation

MDP 이론에 기반한 Bellman 방정식을 이해하여야 한다.

 

고민해야할 것들 : state, value, P(transition probability), R(reward) 코딩

# state는 0~100으로 해야할까 아니면 1~99로 해야할까? 1~99로 한다면 0, 100일 때 Episode종료는 어떻게 코딩할까

state = [1, 2, 3, ,,, , 99]로 하고 s_prime 변수를 만들어 v(s_prime == 0 | s_prime == 100) = 0로 두면 된다. 종료된다는 것이 앞으로 얻을 수 있는 reward 총합이 0이라는 것과 같다.

# s'은 0 또는 100이 될 수 있다. v(s')을 계산해야 하는데 v(0)과 v(100)은 어떻게 둬야 할까?

위에서 이야기 한 것처럼 코딩하면서 자연스럽게 v(0) = v(100) = 0으로 두어야 함을 느끼게 되었다. 

# P 코딩. 간단한 예제의 경우 모든 경우를 손으로 코딩할 수 있지만, 본 문제는 P를 dictionary array 형태로 코딩하면 총 51*50=2550 가지의 state, action 쌍에 대해서 각 2가지의 s'이 존재하므로  51*50*2=5100 가지 경우를 코딩해야 한다.

P(s, a, s')함수를 만들어 이길 경우 0.4를 반환, 질 경우 0.6을 반환하면 된다.

# R 코딩. s' == 100인 경우에만 R = 1이고 나머지 모두의 경우에는 R = 0이다. 이를 함수로 만들고 Value Iteration에서 호출하면 간단할 것 같은데?

 

 

---

21.10.15

[고민과정]

(좌) s, a의 범위와 반복구문의 범위를 고민하였고 (우) s'이 0, 100이 되었을 때 value의 배열범위를 벗어나는 문제에 대해 고민하며 value 범위를 state 0 ~ 100으로 변경하였다.

 

 

 

 

 

21.10.16

[고민과정]

(좌) 나의 결과와 답이 다른 이유는 코드 상에서 s'이 누락되어 정확한 value update가 되지 않기 때문임을 확인하였다. (우) 그래서 action마다의 q(s,a)값을 q배열에 순서대로 저장하여 이 중 max값을 state-value로 저장하는 방법으로 수정하였다. 그리고 그 때의 action을 Optimal Policy 배열에 갱신, 저장하였다.

 

# 문제점 : 마지막 a에 대한 s'만이 저장된다.

# 해결책 : q-value를 따로 만들어서 배열에 a에 따른 q값을 저장하고 각 s에서 max(q배열)을 구한다.

 

 

각 action마다 q-value를 담을 q배열을 만들어 저장하고 action에 대한 for 구문을 마치면 해당 q에서 max값을 v[s]로 저장하여 해결하였다. 또 바로 연이어 해당 max q의 원소순서로 해당 action을 파악해 Optimal Policy로 저장하였다. 이렇게 Value Iteration이 더욱 간결한 코드로 정리되었다. 또, 한번의 value update 과정에서 optimal policy도 찾아지는 과정을 더욱 잘 이해할 수 있었다.

 

[결과그래프]

 

(좌) 수정한 코드로 다시 그린 v*, OptimalPolicy (우) 정답지

 

 

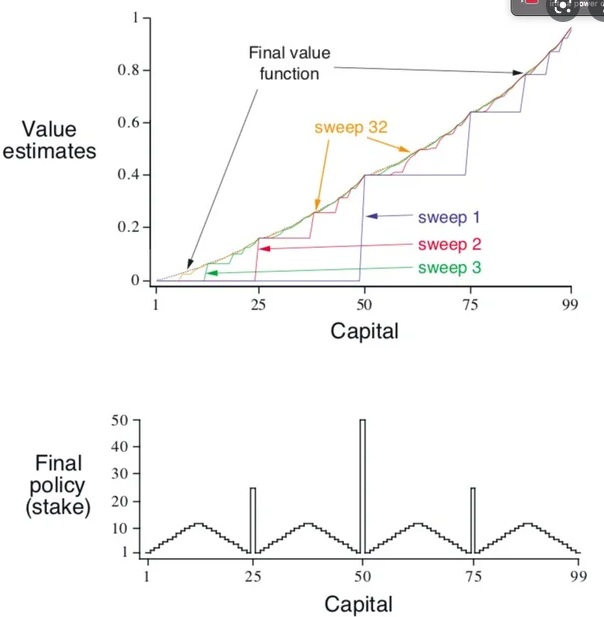
추가 피드백)

1. Optimal Policy 그래프가 보다 더 교재처럼 이쁘게 나오려면 동전이 앞면이 나올 확률(승률)을 0.4에서 0.25로 줄이면 보다 교재와 가까운 그래프를 얻을 수 있다.

그 이유는 승률이 높을 수록 더 많이 자신의 금액을 올인하게 된다. 교재처럼 올인을 억제하기 위해서 승률을 0.25로 낮춤으로써 더 이쁜 그래프를 얻을 수 있다.

 

2. reward 값을 반올림하여 처리하면 더 결과가 좋을 수 있다.

---

Thanks to

1. 포스텍 이승철 교수님. 강화학습 코드 수업

https://www.youtube.com/watch?v=HaBUSk6rat4&list=PLGMtjo8jDX9CjkmQOEUSoY5QMVE-D86pK&index=12 

이론를 공부해도 코드는 처음에 너무 막막했는데 교수님의 강의를 통해서 어떻게 시작해야할지, 식은 어떻게 코드로 나타낼 수 있는지에 대해서 알게 되었다.

2. Google Colab

https://colab.research.google.com/

어디서나 코드를 작성하고 저장하며 과제 수행을 할 수 있었다.