라그랑지안으로 운동방정식 세우기
진동 혹은 동역학적 시스템의 운동방정식을 도출할 때, 1자유도계 시스템에서는 에너지보존법칙 혹은 뉴턴법칙으로 운동방정식을 세울 수 있지만 2계 자유도 시스템 이상에서 부터는 복잡해지�
needs-searcher.tistory.com
본 글은 MIT OCW의 수업내용을 참고했습니다.
한 방향으로만 운동하는 1자유도계 mck시스템의 운동방정식을 뉴턴 제 2법칙이 아닌
지난 글에서 소개한 라그랑지안의 방법으로 구해보도록 하겠습니다.
위 링크된 글의 4. 라그랑지안 메뉴얼의 순서대로 진행하겠습니다.
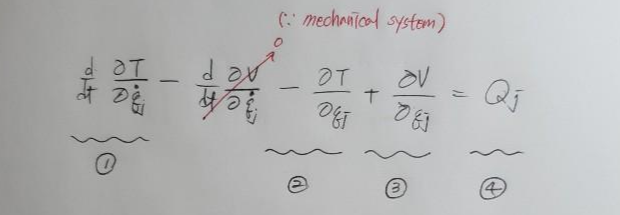
좌변에 대해서)
1. 시스템의 자유도를 결정하고 일반화된 좌표정하기
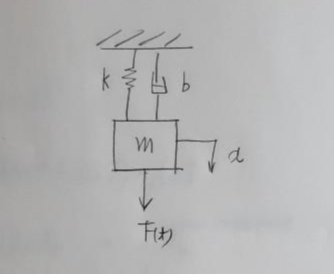
m은 위아래방향으로만 운동하는 1자유도계 시스템이며 아래방향을 +x로 좌표를 잡았습니다.
2. complete, independent, holonomic를 모두 만족하는가?
+x좌표를 통해 m의 움직임을 모든시간에 대해 나타낼 수 있고
1개 좌표이므로 independent하며
시스템의 자유도와 일반화된 좌표수가 1개로 같으므로 holonomic합니다.
3. 운동에너지 T와 위치에너지 V 계산하기

4. ①, ②, ③을 각 q_j에 대해 계산하기
1계자유도 시스템이므로 q_j=q_1=x이므로 x에 대해서만 계산하면됩니다.

우변에 대해서)
1. 각 좌표에 있어서 해당 좌표에 작용하는 총 외부 비보존력을 구합니다.
x좌표에서 작용하는 총 외부 비보존력은 외력 F와 뎀핑힘 bx돗입니다.
중력과 용수철힘은 보존력이므로 제외합니다.
2. 해당 좌표에 작용하는 외부 비보존력(Q_j)을 총 외부비보존력(시그마F)과 좌표방향 단위벡터의 dot product를 통해 구합니다.

식 도출) ①+②+③=④

mg로 인해 용수철이 미소길이만큼 늘어난 정적평형상태에서 생각한다면 용수철힘과 mg값이 상쇄되지만 mg로 인해 용수철이 늘어나기 전부터를 생각하면 mg값이 위 방정식과 같이 남아있게 됩니다.
따라서 위 식은 기계진동에서 보는 mx더블돗+cx돗+kx=F(t)와 같음을 알 수 있습니다!!
1계 자유도 시스템에서는 뉴턴방정식이나 에너지보존법칙을 이용할 때가 라그랑지안보다 더 쉽고 간편합니다.
다음에는 2계 자유도 시스템의 운동방정식을 라그랑지안으로 도출해보도록 하겠습니다.
출처) MIT OCW Engineering Dynamics J. Kim Vandiver
https://www.youtube.com/watch?v=zhk9xLjrmi4
감사합니다.
'기계공학부 시절의 기록 > 제어' 카테고리의 다른 글
| 뇌로 제어하는 로봇 (0) | 2021.04.10 |
|---|---|
| 밸런싱로봇 만들고 싶다 (0) | 2021.04.09 |
| 막대-진자 운동의 운동방정식, 상태공간방정식, 시뮬링크로 해석하기 (0) | 2020.05.28 |
| 라그랑지안으로 운동방정식 세우기 (0) | 2020.05.20 |
| 역진자(inverted pendulum)의 운동방정식 (0) | 2020.05.20 |


댓글