역진자(inverted pendulum)의 운동방정식

자유물체도와 운동방정식 4개

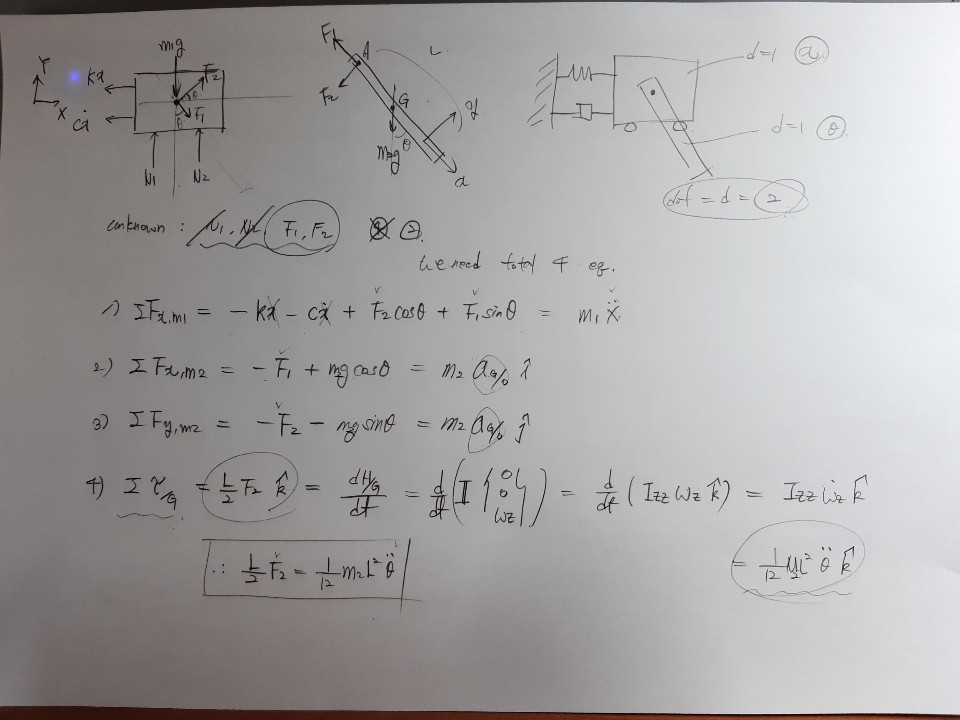
카트와 막대기로 구성된 이 시스템은 2개의 변수로 운동을 나타낼 수 있다. 카트의 수평방향으로의 X, 카트에 핀 고정된 막대기의 회전각도 세타.

수직항력 N1,N2와 핀에서 작용하는 F1,F2로 총 4개의 미지힘이 존재한다.

따라서 2개의 독립변수+4개의 미지힘 총 6개의 방정식이 필요해보인다.

하지만 카트가 수직방향으로는 움직이지 않아 카트의 Y방향 가속도 a_y=0이므로 N1,N2는 고려하지 않아도 된다.

따라서 2개의 독립변수 + 2개의 미지힘 총 4개의 방정식이 필요하다.

 

1. 카트의 X방향 병진운동에 대한 뉴턴 제 2법칙

2. 막대기의 질량중심의 x방향 병진운동에 대한 뉴턴 제 2법칙

3. 막대기의 질량중심의 y방향 병진운동에 대한 뉴턴 제 2법칙

4. 막대기의 질량중심 관점에서의 회전운동에 대한 d(각운동량)/dt=돌림힘 방정식

 

첫번째 사진의 운동방정식에 대입할 원점(O)관점에서 본 질량중심(G)의 가속도를 구한다.

원점에서 바라본 질량중심의 속도는 핀고정된 A점의 병진속도와 A점에서 바라본 G의 속도(회전)의 합이며

이렇게 구한 속도를 시간에 대해 미분함으로써 가속도를 얻는다.

이 때 X방향 단위 벡터 I와 막대기의 길이 L은 변하지 않으므로 상수취급한다.

또, 좌표축의 미분은 각속도벡터와 좌표축의 벡터곱이다.

마지막으로 막대기의 좌표인 i j로 정리한다.

 

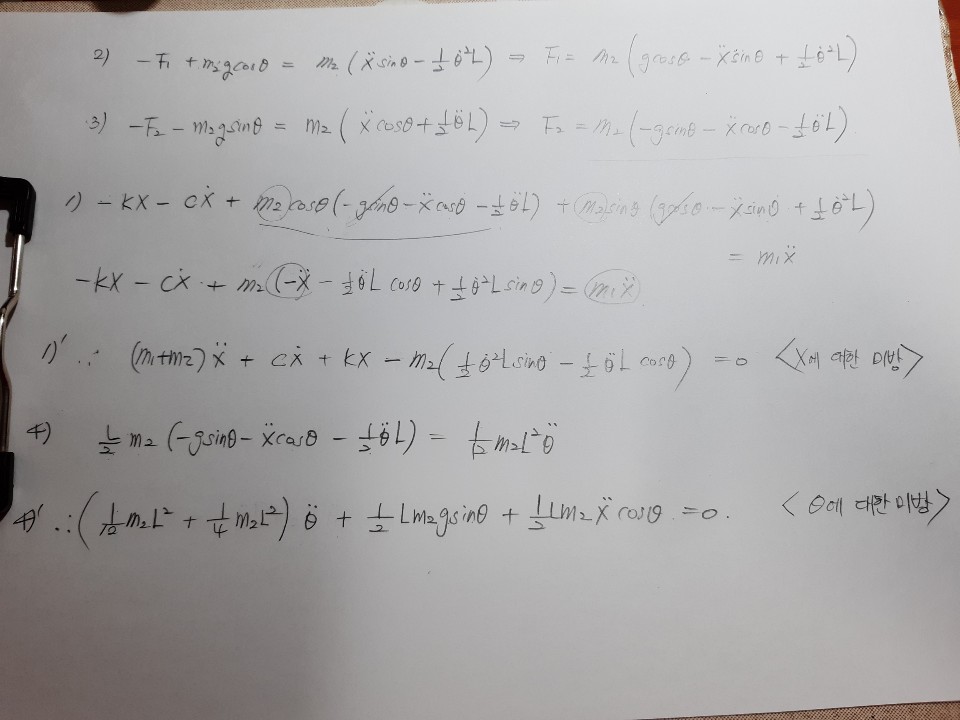
대입과 정리를 통해 1'와 4'로 독립변수 X와 세타에 대한 두개의 비선형 미방형태의 운동방정식이 도출되며

세타가 매우 작을 때를 가정하면 sin세타=세타, cos세타=1로 정리하여 선형미방으로 정리가 된다.

 

 

기계공학 전공 재료 열 유체 동 역학 응용역학 상담 드립니다. | 5000원부터 시작 가능한 총 평점 0

 

 

출처) MIT OCW Engineering Dynamics  J. Kim Vandiver

https://ocw.mit.edu/courses/mechanical-engineering/2-003sc-engineering-dynamics-fall-2011/finding-equations-of-motion-for-rigid-body-rotation/

Finding Equations of Motion for Rigid Body Rotation | Engineering Dynamics | Mechanical Engineering | MIT OpenCourseWare

 

감사합니다.