비회전 유동일 때, 베르누이(Bernoulli)방정식과 속도 포텐셜

1. 비회전 유동의 의미와 수학적 정의

비회전 유동이라는 것은 어떤 것일까요?

비회전 유동이라는 것은 유체 입자가 회전하지 않고 운동하는 유동을 의미합니다.

 

유선이 곡선이지만 유체입자는 회전하지 않고 유선을 따라 흐를 수 있습니다.

유선이 직선이지만 유체입자는 회전하며 유선을 따라 흐를 수도 있습니다.

 

비회전의 수학적 정의

 

 

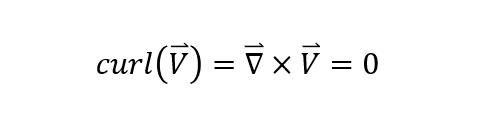
비회전 유동일 때 베르누이 방정식의 제약조건 유선을 따라서만 적용 가능함이 사라지고, 속도포텐셜이 존재할 수 있습니다.

 

2. 비회전 유동의 베르누이방정식

비점성 유체를 가정한 오일러 운동방정식에서 정상상태가정, 비압축성 가정을 하였을 때 V X 델 X V (X:크로스곱)을 0으로 만들기 위해 유선방향의 미소길이 ds를 곱했지만 비회전일 경우 델 X V = 0 이므로 ds가 굳이 유선방향이 아니여도 된다. 따라서 유동장 전체에 걸쳐서 베르누이방정식을 적용할 수 있다.

비점성, 정상상태, 비압축성, 비회전의 베르누이방정식. 유동장전체에 걸쳐 적용가능하다.(유선을 따라서만 적용할 필요 없다.)

 

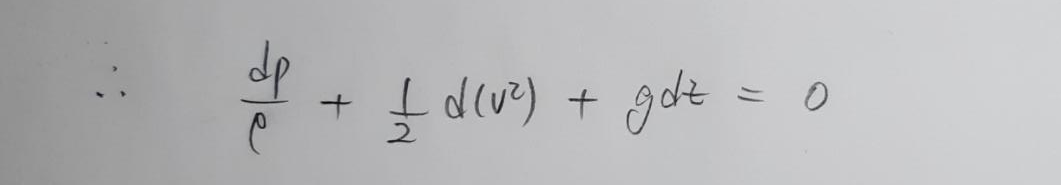
3. 속도 포텐셜

속도 포텐셜은 마치 보존력이 작용할 때 존재하는 포텐셜의 개념과 유사합니다.

Potential Theory (퍼텐셜 이론)

간단히 정리하자면 3차원공간에서 위치에너지를 정의하기를 어떤 Scalar값(위치에너지)를 변위에 대해 미분하고 -를 곱한 값이 작용하는 힘이 될 때 공간상 두 지점사이를 하나의 함수, Potential로 정의할 수 있었고 그 힘 F = -gradient(V) 이므로 Curl(F)=0를 만족했습니다. 따라서 보존력인지 아닌지 확인하는 방법은 Curl(F)=0인지 확인하는 것이었습니다.

 

가정1. 비회전유동

마찬가지로 오늘 배운 유체의 속도장이 Curl(속도장 벡터)=0을 만족하는 비회전유동일 경우 해당 속도장의 Potential이 존재하고 이를 속도포텐셜이라 정의합니다. Curl(속도장 벡터)=0을 만족하기 위해서는 속도장벡터는 스칼라값의 미분이어야 합니다. 이를 표현한 것이 속도 포텐셜의 정의와 같습니다. 

 

속도퍼텐셜의 정의 (스칼라 표현)

속도퍼텐셜의 정의 (벡터 표현)

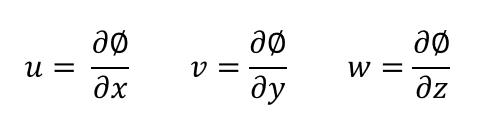
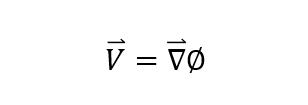
이 식은 위치에너지가 정의 되기 위한 필요충분조건과 거의 똑같습니다.

위치에너지의 필요충분조건

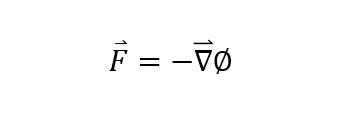
4. 유동함수와의 비교

유동함수를 통해 유량을 계산하고 원통좌표계로 표현하기

유동함수는 연속방정식으로 부터 

가정1. 정상상태

가정2. 비압축성

가정3. 평면(2차원) 유동

이 3가지 조건을 취한 연속방정식에서 2차원 평면상에서 위치에 대해 하나의 스칼라 값을 가지는 함수를 정의하여 공간상에서 유동함수를 이용해 유동의 운동, 속도를 나타내었고 유선을 그릴 수 있었으며 유량역시 구할 수 있었습니다.

 

속도퍼텐셜은 비회전유동에 기인합니다.

그리고 이 속도퍼텐셜을 통해서 유동함수가 못하는 3차원에서의 유체운동을 나타낼 수 있습니다.

 

5. 라플라스 방정식

정상/비정상, 압축성/비압축성 모두에서 유효한 연속방정식(질량보존법칙)

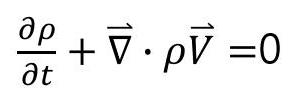
위의 연속방정식으로부터 

가정1. 비압축성

을 적용하면 아래 식과 같습니다. 

비압축성. 연속방정식

가정2. 비회전 유동일때 속도퍼텐셜이 존재하고 이를 위 연속방정식에 대입하면 라플라스방정식입니다.

라플라스방정식

 

정리하면

가정1. 비압축성

가정2. 비회전 유동

의 경우에 라플라스 방정식을 쓸 수 있으며 

가정3. 비점성 유체 를 추가하면 전체 유동장에 대해 베르누이방정식을 적용할 수 있습니다.

 

감사합니다.

 

 

기계공학 전공 재료 열 유체 동 역학 응용역학 상담 드립니다. | 5000원부터 시작 가능한 총 평점 0

 

 

출처)

YOUNG MUNSON OKIISHI HUEBSCH 쉽게배우는 유체역학 5판 (WILEY, 홍릉과학출판사)

 

금오공대 KOCW 유체역학2 박준영 교수님 비점성유동

http://www.kocw.net/home/cview.do?lid=dd24d2e7aa7876ab

유체역학2