정상, 비정상, 압축성, 비압축성 모두에서 유효한 연속방정식에서 시작합니다.

가정. 정상상태, 비압축성, 평면(2차원)유동
여기서 정상상태, 비압축성, 평면, 즉 2차원 유동으로 가정합니다.
이는 가장 단순하면서도 실제에 유용하며 파이프 운동이나 회전 물체 주위의 유동과 같은 축대칭 유동과 2차원 압축성 유동들에 대해서 적용되는 유동함수를 유도하기 위함입니다.
위 가정으로 연속방정식이 어떻게 간단화되는지 보겠습니다.
먼저 정상상태이므로 첫째항인 밀도의 시간 편미분은 0이됩니다.
또, 비압축성이기 때문에 둘째항의 밀도가 결과적으로 없어집니다. 그러면 아래와 같이 됩니다.

또 여기서 마지막으로 2차원 유동이므로 z축을 고려하지 않습니다. 그러면 아래와 같이 됩니다.

여기서 스칼라값인 유동함수를 정의할 것입니다. 이는 유동함수로 나타난 유동은 항상 질량보존법칙을 만족함을 의미합니다.
유동함수는 왜 정의될까요? 두가지가 있습니다. 첫번째는 2차원 평면에서 각 위치(x,y)에 따라 x방향 속도인 u와 y방향 속도인 v가 있는데 이를 하나의 스칼라로 표현하기 위함입니다.
두번째로는 이 하나의 스칼라, 즉 유동함수가 일정한 선들은 유선입니다. 즉 2차원 평면에서 유동함수를 통해 유선을 그릴 수가 있는 것이죠!!
그 유동함수의 정의는 다음과 같습니다.

이 유동함수가 일정한 선은 유선이 된다고 했는데요 이를 또 유도해보겠습니다.

정리해보면 2차 평면에서의 유동함수를 안다면 이로부터 유선을 그릴 수 있다는 것입니다.
그리고 그렇게 그려진 유선들에서 유동함수_a에 의해 그려진 유선과 유동함수_b에 의해 그려진 유선사이에 흐르는 유체의 유동을 구할 수 있습니다.

따라서 dq는 차이가 작은 유동함수 사이를 지나는 유량으로
유량 q는 아래와 같다.

이제 드디어 마지막으로 원통좌표계입니다.
지난 글에서 다룬 미분형태의 연속방정식과 오늘 글의 유동함수를 원통좌표계를 이용해 나타내보겠습니다.

자 이렇게 원통좌표계는 r, z, 세타를 가지고 공간에 위치한 점p를 나타냅니다.
여기서 미소 유체요소를 잡은뒤 직각좌표계에서 연속방정식을 유도했던 과정을 똑같이 진행합니다.
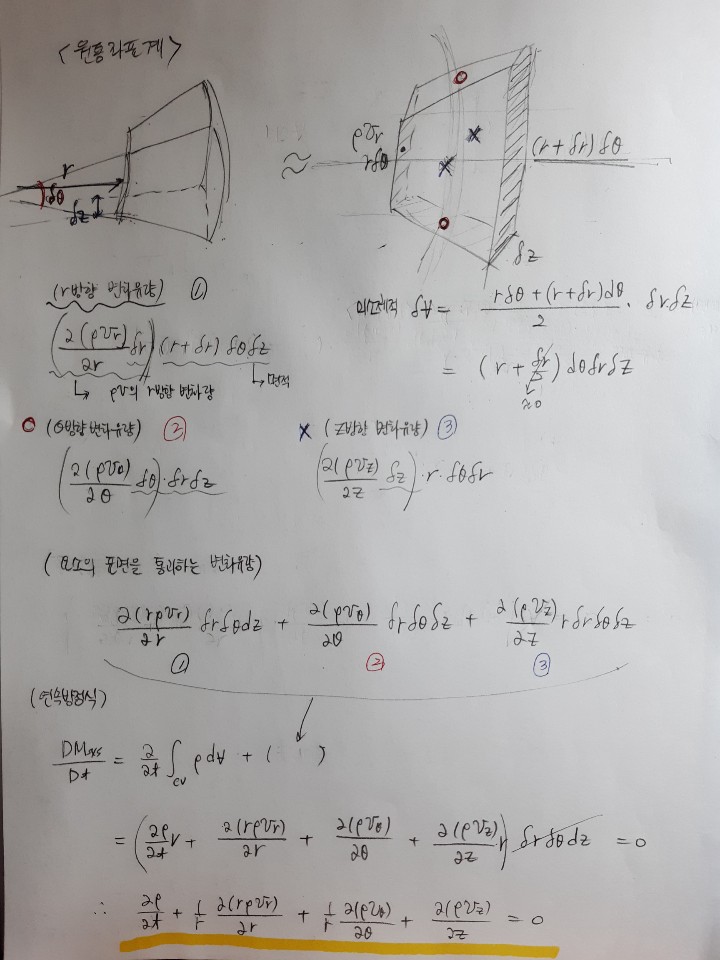

비압축성으로 밀도의 시간에 대한, r방향에 대해, 세타방향에 대한 편미분은 0이되고
2차원 유동으로 한정시킴으로써 z항은 고려하지 않습니다
따라서 위와 같은 식이 나옵니다.
여기서 또한 유동함수를 정의할 수 있고 비압축성, 2차원 유동의 연속방정식을 만족합니다.

하지만 주의할 것은 유동함수는 파이프 유동이나 회전물체 주위의 유동, 축대칭 유동, 2차원 유동을 제외한 일반적인 3차원 유동에 대해서는 적용되지 않습니다.!!
기계공학 전공 재료 열 유체 동 역학 응용역학 상담 드립니다. | 5000원부터 시작 가능한 총 평점 0
0개 총 작업 개수 완료한 총 평점 0점인 니즈서쳐의 직무역량, 기타 직무역량 레슨 서비스를 0개의 리뷰와 함께 확인해 보세요. 직무역량, 기타 직무역량 레슨 제공 등 5000원부터 시작 가능한 서
kmong.com
출처) YOUNG MUNSON OKIISHI HUEBSCH 쉽게배우는 유체역학 5판 (WILEY, 홍릉과학출판사)
'기계공학부 시절의 기록 > 유체역학2' 카테고리의 다른 글
| 오일러 운동방정식(Euler motion equation) 유도하기 (0) | 2020.06.01 |
|---|---|
| 미분형 선형운동량 방정식, 왜 필요해? (0) | 2020.05.13 |
| 질량보존법칙에서 연속방정식을 유도하고 미분형으로 나타내기 (2) | 2020.05.11 |
| 유체입자의 운동학 : 각변형(Angular deformation) (0) | 2020.05.06 |
| 유체입자의 운동학 : 선형변형 (0) | 2020.05.06 |




댓글