지난 글에서 유체운동은 병진, 선형변형, 각변형, 회전으로 모두 표현할 수 있으며
각각에 대해 대략의 개념을 나타내었다.
유체입자의 운동학 Intro : 병진, 선형변형, 각변형, 회전 그중 병진운동
유체입자의 운동은 4가지로 모두 표현할 수 있다. 병진과 회전으로 이루어진 강체의 운동과 달리 유체는 변형이 보다 자유롭게 일어나 선형변형과 각변형이 있다. -병진운동은 유체의 변형이 없
needs-searcher.tistory.com
이번 글에서는 선형변형을 알아보자.
요약)
우리는 관찰된 유체의 속도장에서
공간이동에 대한 속도의 변화를 보고
유체의 운동을 병진, 선형변형, 각변형, 회전으로 나누어 해석하려고 한다.
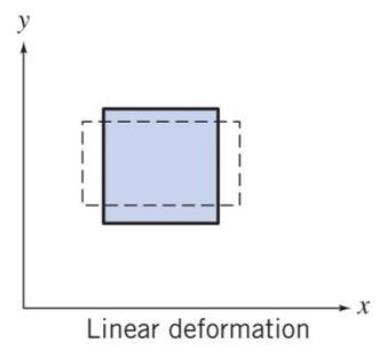
선형변형은 위 그림과 같이 가로축으로 인장 압축 또는 세로축으로 인장 압축이 일어나는 경우이다.
'주어진 속도장에 따른 유체의 체적변화는 어떻게 될까?'가 선형변형의 주 관심사이다.
또, 중요한 것은 비압축성 유체일 경우에 질량은 보존되므로 체적변화율은 0이라는 것이다.
본 글에서 유체의 속도장과 유체의 단위부피당 체적변화율의 관계식을 알아보자.


출처)
-WILEY 쉽게배우는 유체역학 5판 홍릉과학출판사
-서울대 유체역학 및 기계 pdf자료
file:///C:/Users/Ju%20Hyeong/Downloads/%EC%9C%A0%EC%B2%B4%EC%97%AD%ED%95%992016%20%EC%A0%9C4%EA%B0%95-%EA%B2%80%EC%82%AC%EC%B2%B4%EC%A0%81%20%EB%AF%B8%EB%B6%84%EB%B0%A9%EC%8B%9D.pdf
'기계공학부 시절의 기록 > 유체역학2' 카테고리의 다른 글
| 유동함수를 통해 유량을 계산하고 원통좌표계로 표현하기 (0) | 2020.05.11 |
|---|---|
| 질량보존법칙에서 연속방정식을 유도하고 미분형으로 나타내기 (2) | 2020.05.11 |
| 유체입자의 운동학 : 각변형(Angular deformation) (0) | 2020.05.06 |
| 유체입자의 운동학 Intro : 병진, 선형변형, 각변형, 회전 그중 병진운동 (0) | 2020.05.06 |
| 물질도함수, 라그랑지안이야 오일러야??? (5) | 2020.05.04 |




댓글