선형변형 복습 + 각변형 요약)
우리는 관찰된 유체의 속도장에서
공간이동에 대한 속도의 변화를 보고
유체의 운동을 병진, 선형변형, 각변형, 회전으로 나누어 해석하려고 한다.
지난 글에 소개한 선형변형은 x방향으로는 x방향의 속도만 변했고 y,z방향 역시 마찬가지였다.
그 결과 체적변화가 일어날 수 있지만 비압축성 유체의 경우 체적변화율=0이었다.
속도장과 체적변화률의 관계식은 다음과 같았다.

각변형의 경우는 반대로
x방향으로 y방향의 속도가 변하고, y방향으로는 x방향으로의 속도가 변할 때 나타난다.
(물론 선형변형도 함께 나타날 수 있지만 각변형만을 관찰하고자 단순화한다.)
이 때, 주어지는 속도장으로부터 유체가 회전하는지, 각변형을 일으키는지 수식으로써 확인할 수 있다.
1. 유동의 대표각속도(부호규약이 매우 중요하다.)

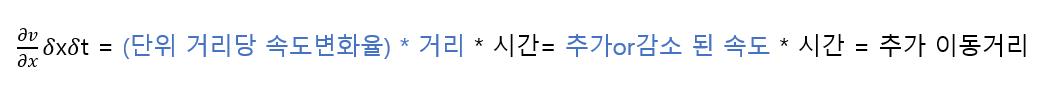

그리고 x,y,z축의 대표 각속도를 각각 i,j,k방향으로 w벡터를 나타낸다.
2.유동의 회전 = curl V벡터

curl V벡터가 = 0 이라는 것은 회전을 하지 않는다는 의미이다.
그런데 여기서 3차원공간에서 보존력이 작용할 때 위치에너지가 존재하고 역학적에너지가 보존됨을 상기시켜보면 이를 위한 필요충분조건은 다음과 같고

이 때 Curl F = 0이 됩니다.
3차원에서의 보존법칙
요약) 1차원에서와 달리 3차원에서는 위치에너지를 일반적으로 정의할 수 없다. 보존력이 작용하는 경우에만 3차원에서의 위치에너지를 정의할 수 있으며 보존력이 작용할 때 3차원에서 에너지가 보존된다. 1. 1차..
needs-searcher.tistory.com
즉, 이를 속도장과 유동의 회전에 적용하면
속도장 벡터가 어떤 Scalar값의 Gradient일 때, curl V = 0 이 되고 비회전유동이 됩니다.
비회전 유동은 유동해석을 매우 간단하게 만들어준다는 면에서 중요합니다.
이 부분이 조금 어렵지만 다시 정리를 해보면,
3차원공간에서 위치에너지를 정의하기를 어떤 Scalar값(위치에너지)를 변위에 대해 미분하고 -를 곱한 값이 작용하는 힘이 될 때 공간상 두 지점사이를 하나의 함수, Potential로 정의할 수 있었고 그 힘 F = -gradient(V) 이므로 Curl(F)=0를 만족했습니다. 따라서 보존력인지 아닌지 확인하는 방법은 Curl(F)=0인지 확인하는 것이었습니다.
마찬가지로 오늘 배운 유체의 속도장이 Curl(속도장 벡터)=0을 만족하는 비회전유동일 경우 해당 속도장의 Potential이 존재할 것이라는 것을 짐작할 수 있습니다.
이는 곧 다시 다룰 기회가 있을 것 같습니다.
-WILEY 쉽게배우는 유체역학 5판 홍릉과학출판사
'기계공학부 시절의 기록 > 유체역학2' 카테고리의 다른 글
| 유동함수를 통해 유량을 계산하고 원통좌표계로 표현하기 (0) | 2020.05.11 |
|---|---|
| 질량보존법칙에서 연속방정식을 유도하고 미분형으로 나타내기 (2) | 2020.05.11 |
| 유체입자의 운동학 : 선형변형 (0) | 2020.05.06 |
| 유체입자의 운동학 Intro : 병진, 선형변형, 각변형, 회전 그중 병진운동 (0) | 2020.05.06 |
| 물질도함수, 라그랑지안이야 오일러야??? (5) | 2020.05.04 |




댓글