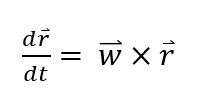
회전축을 중심으로 회전하는 강체의 하나의 질점을 밖에서 본 속도는 위의 식과 같다.
크기가 일정하고 방향이 일정한 각속도는 그냥 저식을 쓰면 된다.
하지만 각속도의 크기와 방향이 시간에 따라 변한다면 그 각속도는 어떻게 우리가 정의할 수 있을까
핵심은 매순간 변하는 각속도를 변하기 전의 각속도의 방향좌표를 이용해 나타내는 것이다.
이렇게 한다면 하나의 좌표축으로 변하는 각속도를 계속해서 표현할 수 있다.
바로 시작해보자

위와 같이 강체의 각속도가 변한다.
매순간 강체에 올라탄 관점에서 r은 속도가 없으며 밖에서 본 r의 속도는 그 순간의 각속도와 위치벡터의 외적이다.
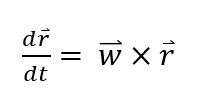
문제는 이 w가 변하는 것이고 우리는 이를 e벡터로 계속해서 나타내고 싶은 것이다.
교수님의 말씀을 인용하면 더 이해가 쉬울 것 같다.

즉, 각속도가 변하기 전의 좌표축으로 변한 각속도를 고대로 표현할 때
변한 각속도의 방향벡터는 어떤 행렬과 기존 각속도의 방향벡터의 선형결합으로 나타내어질 수 있어야하고
기존 좌표축벡터와 그것의 시간미분의 관계는 다음 식과 같다.

이렇게 식으로 보면 잘 안와닿는다. 선형대수에서는 벡터를 행렬처럼 다음과 같이 쓰는것 같다.

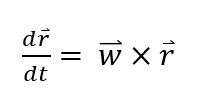
a로 이루어진 저 행렬을 구체적으로 정의할 수 있다면 우리는 변하는 각속도에 대해서 아래식을 쓸 수 있을 것이다.
자 다시 아래의 식에서 계속해보자

지금 하려고 하는 것은 행렬 a_ij를 구체적으로 계산하기 이다.
양변에 e_j벡터를 dot product하면 다음과 같다

여기서 우변의 e_j벡터가 사라진다!!?
그 이유는 e방향벡터는 크기가 1인 단위벡터이고 e_j와 e_j. 즉 방향이 같은 단위벡터의 dot product이므로
1이된다.
a_ij와 a_ji의 관계를 알기위해 다음식을 생각해본다.
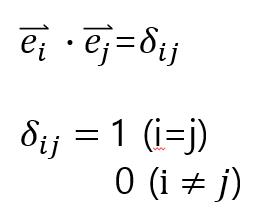
e_i 와 e_j는 서로 같은 방향벡터이므로 dot product를 했을 때 i와 j가 같을 때는 1이 되고 서로 다를 때는 0이 된다.
선형대수에서 크로네커 델타라 부른다.
이 식을 시간에 대해 양변을 미분해보자
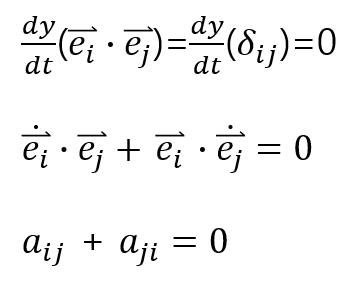
마지막 식에서 알 수 있는 것은 행렬 a가 Antisymmetric하다는 것이다.
행렬이 Antisymmetric하면 행렬의 대각방향은 0이 되고 총 9개의 서로다른 수가 아닌 3개의 서로다른 수로 행렬이 구성된다. 이는 3차원에서 3개의 독립변수를 가지고 방향을 나타내는 벡터와 대응되어 마치 벡터처럼 쓸 수 있다.
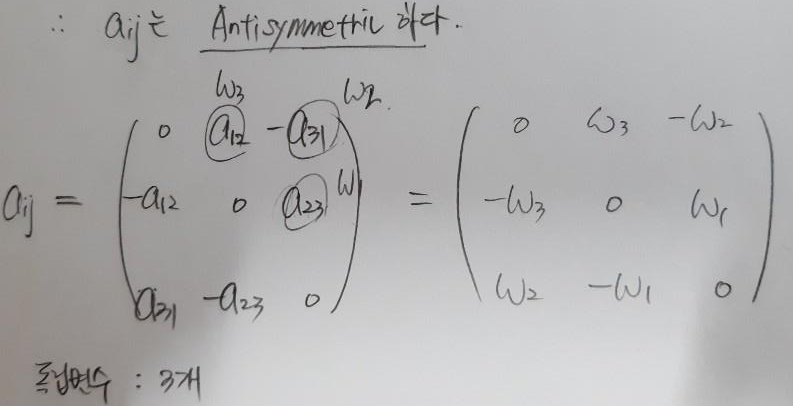
왜 a11, a22, a33이 모두 0이 되는지는 (행렬a+행렬a)의 11성분은 a11+a11=0 이고 나머지도 마찬가지이며
다시 이 행렬을 2로 나누어주면 행렬a는 위와 같이 된다.
총 3개의 독립변수로 이루어진 행렬a를 각속도 w1, w2, w3로 정의하면 최종적으로 위와 같이 a행렬을 나타낼 수 있다.
이제 마지막으로 이렇게 구한 것을 바탕으로 r벡터의 속도를 구해보면 결과적으로
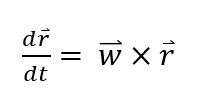
임을 알 수 있다.

출처) 한양대학교 KOCW 고전역학2 신상진 교수님 강의 1차시 강체의 회전
'기계공학부 시절의 기록 > 고전역학2' 카테고리의 다른 글
| [고전역학] 각운동량의 미분 그리고 세차운동(precession) (0) | 2020.05.17 |
|---|---|
| [고전역학] 주축(Principal axis)의 정의와 고유값 방정식(eigenvalue eq.) (0) | 2020.05.17 |
| [고전역학] 강체의 운동에너지, T=wJ/2 (0) | 2020.05.14 |
| [고전역학] 대각화 : 주축(Principal axis)로 축을 회전시키다. (0) | 2020.05.14 |
| [고전역학] 관성 텐서(inertia tensor)와 관성모멘트(I=mr^2)의 관계, 각운동량 J=Iw 유도 (0) | 2020.05.13 |




댓글