
회전하는, 회전축이 기울어진 팽이는 위 그림과 같이 회전축 자체가 한 축을 중심으로 회전합니다. 이러한 운동을 세차운동이라고 합니다.
수업에서는 팽이에 채찍질을 가하지 않아 팽이의 회전속도는 일정하며 각운동량의 축이 회전축과 일치하다는 가정을 했습니다.
이러한 세차운동은 중력으로인한 돌림힘에 의해 발생합니다.
위 그림에서 R벡터와 중력의 크로스product가 돌림힘이며 팽이의 질량중심을 지면으로 들어가는 방향으로 밀어줍니다.
(각질점에 대해 각각 계산하여 다 더하는 것은 도심의 정의에 의해 질량중심에 대한 계산과 동일합니다.)
때문에 팽이의 회전축은 크게 회전을 하게 됩니다.
이를 보이기 위해서 각운동량의 미분의 힘에 관련된 식과 운동에 관련된 식을 사용합니다.
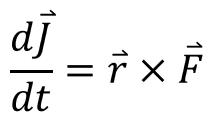
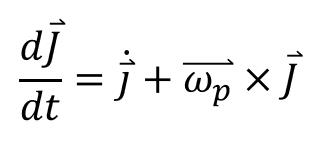
(밖에서 보았을 때의 각운동량의 속도)= (회전축에 고정된 좌표계에서 바라본 각운동량 자체의 속도)+(밖에서 바라본 각운동량의 축의 회전각속도)X(각운동량) 입니다.
이를 이해하기 위해서는 아래 글에서 '바깥에서 바라본 회전축에 고정된 벡터의 속도'를 참고하시길 바랍니다!
코리올리힘은 가짜힘(2) : 코리올리힘 계산하기_수식포함
요약) -일정한 각속도(w)로 회전하는 계에 고정된 r벡터의 속도와 가속도를 구한다. -지구 바깥에서 바라봤을 때 나타나는 추가적인 가속도항을 발견할 수 있다. -이 가속도가 가상힘 코리올리 힘
needs-searcher.tistory.com
먼저 각운동량의 미분에 관한 운동식을 유도하고 각운동량의 미분과 돌림힘을 운동식의 형태로 만들어 w_p, 밖에서 본 회전축의 회전속도(세차운동 속도)를 구합니다.
1. 각운동량의 미분에 관한 운동식 유도

위 필기에서의 w는 세차운동의 각운동량 축 자체의 회전속도입니다.
또, 팽이의 회전속도는 일정하므로 w돗=0 이고 따라서 J돗=0입니다.
이제 위 필기의 w, 세차운동의 각속도를 구하면 됩니다.
2. 각운동량의 미분-돌림힘 식을 운동식 형태로 하여 세차운동 속도 구하기

위 필기에서는 세차운동의 각운동량 축의 자체회전속도를 큰 오메가(옴)으로 표시했습니다.
이를 통해 팽이의 회전축은 큰 오메가의 각속도로 회전하며 방향은 k방향이며 관성모멘트가 클수록 느리고 중량과 원점으로부터의 거리가 클수록 빠름을 확인할 수 있습니다.
출처) 한양대 KOCW 신상진 교수님 고전역학2 3차시 관성모멘트 계산, 세차운동
http://www.kocw.net/home/search/kemView.do?kemId=1278708
고전역학2
www.kocw.net
'기계공학부 시절의 기록 > 고전역학2' 카테고리의 다른 글
| [고전역학] 주축에 대한 관성모멘트 계산(feat. 관성텐서, 평행축이론, 육면체, 구, 원기둥) (0) | 2020.05.17 |
|---|---|
| [고전역학] 주축(Principal axis)의 정의와 고유값 방정식(eigenvalue eq.) (0) | 2020.05.17 |
| [고전역학] 강체의 운동에너지, T=wJ/2 (0) | 2020.05.14 |
| [고전역학] 대각화 : 주축(Principal axis)로 축을 회전시키다. (0) | 2020.05.14 |
| [고전역학] 관성 텐서(inertia tensor)와 관성모멘트(I=mr^2)의 관계, 각운동량 J=Iw 유도 (0) | 2020.05.13 |




댓글